バイアスとは
バイアスとは結論や推論における系統誤差のことを呼びます。
研究の過程では真の結果との差が生じます。
その誤差が系統的に生じることを系統誤差と呼びます。
バイアス=系統誤差=偏り
研究を行うにあたり、全国民や全患者を対象として臨床研究を行うのは
不可能なので、母集団の一部を対象(標本)としてその結果から知りたい値を
推測します。その研究の過程でバイアス・誤差が生じます。

研究で真実(真の値)を知るために、研究して測定したのに誤差が生じて
真実が歪んでしまうリスクを回避するためにこのバイアスの影響を
少なくする必要があります。
よって研究の邪魔をする誤差(バイアス)が入らないように
研究者は研究をデザインをします。
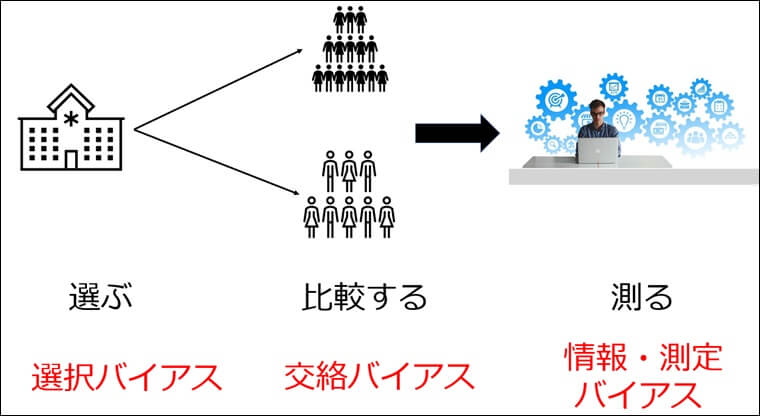
具体的に3つの点に注意する必要があります。
- 対象者を正しく選ぶ
- 正確に測る
- 公平に比較する
臨床で働く理学療法士が論文を読む際は上の3つの点のバイアスが
入ってないかを確認しながら読む必要があります。
主なバイアスは
選択バイアス
情報・測定バイアス
交絡バイアス
この3つとなります。
選択バイアス
選択バイアスは対象を選択する際に生じるバイアスです。
対象者の選び方(サンプリング)に偏りがあると、一般的な患者層を代表していないため
結果に「ずれ・誤差」が出てきます。よって、結果の信頼性が低下します。
理想的には母集団(全体)と標本にギャップがない事なので、
論文を読む際は選択バイアスの影響を考慮する必要があります。
選択バイアスを少なくする方法は
①ランダム化割り付けをする
②割付の隠蔽化をする
③取り込み基準、除外基準を定義する
ランダム化割り付けをする
対象者からランダム(無作為)に介入群とコントロール群に割り付けることで
治療以外の要素を均等にすることができます。
割付の隠蔽化をする
対象者を介入群とコントロール群に割り付ける担当者に、ランダム割り付け表が
隠されている確認しましょう。
隠蔽化されていないと、先入観により割り付ける際に影響が生じる恐れがあります。
取り込み基準、除外基準を定義する
研究の対象者が母集団を反映させるために対象者の取り込み、除外基準を定義します。
例えば膝OAの研究であれば
取り込み基準
・発症から1カ月以上経過
・レントゲン画像でKLステージ2以上
・荷重時痛あり
・膝関節に可動域制限あり
除外基準
・急性外傷による膝痛
・リウマチ
・認知症
取り込み基準・除外基準がしっかり定義されていることが重要です。

論文を読む際はランダム割り付けと割り付けの隠蔽化が
されているか確認しましょう。
情報・測定バイアス
情報バイアスとはデータなどの情報を得る際に生じるバイアスです。
割り付けられたグループがどんな治療を行っているのか
結果(アウトカム)の評価者、解析者のいずれかが知っていると
主観・先入観が生じて判断の客観性が低下するリスクがあります。
情報・測定バイアスを少なくする方法は
・盲検化する
盲検化する
盲検化とはブラインディングまたはマスキングとも呼ばれており、
データ収集の過程で評価者やデータ解析者に情報を伏せることです。
アウトカム測定者がグループの治療内容を知っていると
過大評価・過小評価する可能性があるため、
盲検化がとても重要となります。

論文を読む際は盲検化されているか確認しましょう。
交絡バイアス
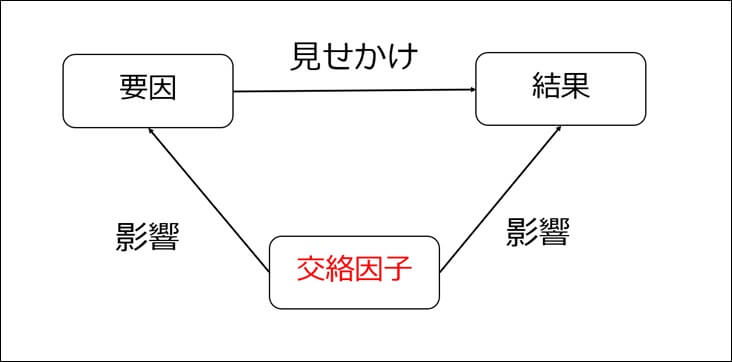
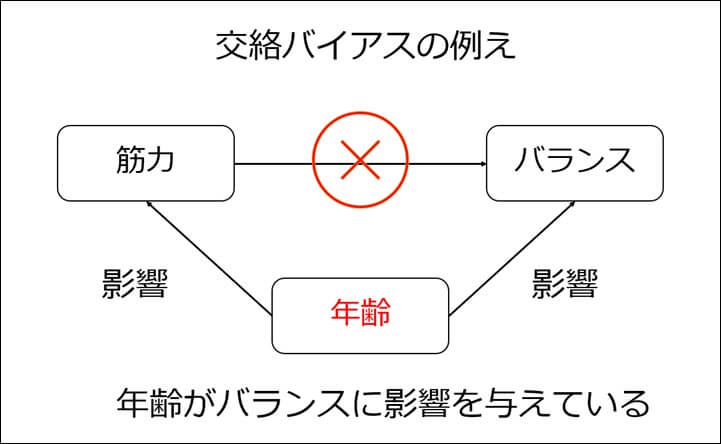
交絡バイアスとは2つのデータ間に本当は直接関連がないのに
第三の要因(隠れた要因)によって、一見関連があるように
見えてしまうことを呼びます。
理想的な研究は治療以外は平等・フェアにすることです。
交絡バイアスを少なくする方法は
・ITT解析を行う
・治療以外は同等にする(マッチングをする)
・ランダム割り付けする
ITT解析を行う
ITTとはIntention To Treatの略であり、「意図された通りの治療」の意味となります。
ITT解析とは研究の初めに割り付けた治療群・コントロール群を研究終了時にも
変えずに解析する手法です。
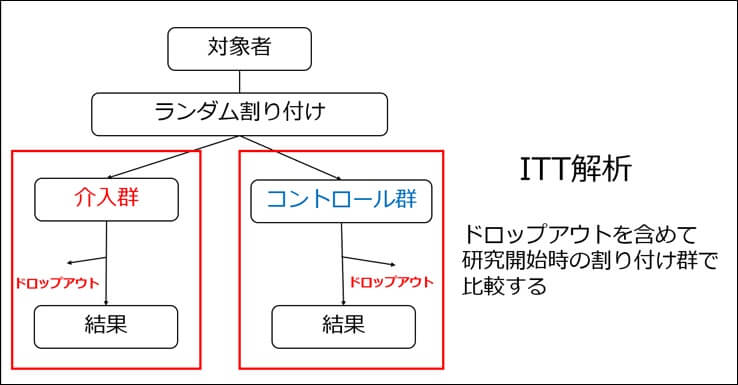
ITT解析することで交絡因子を少なくすることができます。
治療以外は同等にする(マッチングをする)
調べたい要因以外を平等にすることで交絡バイアスを減らします。
交絡因子を揃えることを研究用語でマッチングと呼びます。
年齢、性別、疾患の重症度など患者の背景因子を均等にします。
マッチングすることで交絡因子を少なくすることができます。

論文を読む際はITT解析とマッチングされているか
確認しましょう。
まとめ
今回は論文を読むうえで知るべきバイアスについて説明しました。
論文を正しく読むうえでとても重要なので今回を機会に勉強して
もらえたらと思います。

こちらに記事でも論文の読み方を紹介しているので
参考にしてみて下さい。
統計学について体系的に学びたいかたは対馬 栄輝 先生が講義している
オンラインセミナー リハノメがおすすめです。
第12回までにわたっての講義が視聴可能です。
統計学の基本からリハビリへの活かし方など幅広く学べると思います。
リハノメについてはこちらのブログに詳しく書いてあります。





コメント